Capítulo 6: Introducción a las redes neuronales y el aprendizaje profundo
6.1 Perceptrón y Perceptrón de Múltiples Capas
¡Bienvenido al emocionante y rápidamente avanzado mundo de las redes neuronales y el aprendizaje profundo! Este capítulo marca un cambio significativo en nuestro viaje a medida que nos movemos de las técnicas tradicionales de aprendizaje automático al ámbito del aprendizaje profundo, que es una subcategoría del aprendizaje automático. Debido a su potencial, el aprendizaje profundo ha estado a la vanguardia de muchos avances recientes en la inteligencia artificial, con su capacidad para habilitar autos autónomos, asistentes de voz, recomendaciones personalizadas y mucho más.
En este capítulo, comenzaremos por presentar el bloque básico de construcción de las redes neuronales: el perceptrón. Este es una estructura simple que nos puede ayudar a entender estructuras más complejas como los perceptrones de múltiples capas. Luego, avanzaremos hacia estructuras más complejas y discutiremos cómo forman la base de modelos de aprendizaje profundo más avanzados. También cubriremos los conceptos clave y principios que sustentan estos modelos, incluyendo la retropropagación (backpropagation) y el descenso de gradiente (gradient descent), que son fundamentales para el funcionamiento de las redes neuronales.
Además, después de proporcionar una base sólida en redes neuronales y aprendizaje profundo, profundizaremos en temas más avanzados, incluyendo redes neuronales convolucionales y redes neuronales recurrentes, que son esenciales para comprender cómo se pueden utilizar modelos de aprendizaje profundo en el mundo real. También exploraremos cómo se utilizan estos modelos en el procesamiento del lenguaje natural, la clasificación de imágenes y el reconocimiento de voz. Al final de este capítulo, estarás bien preparado para abordar los temas más avanzados que te esperan en el emocionante mundo del aprendizaje profundo.
¡Así que sumérgete y embarquemos en este fascinante viaje de descubrimiento!
6.1.1 El Perceptrón
El perceptrón es la forma más simple de una red neuronal. Fue introducido por Frank Rosenblatt a finales de la década de 1950. Un perceptrón toma varios inputs binarios, x1, x2, ..., y produce una única salida binaria:
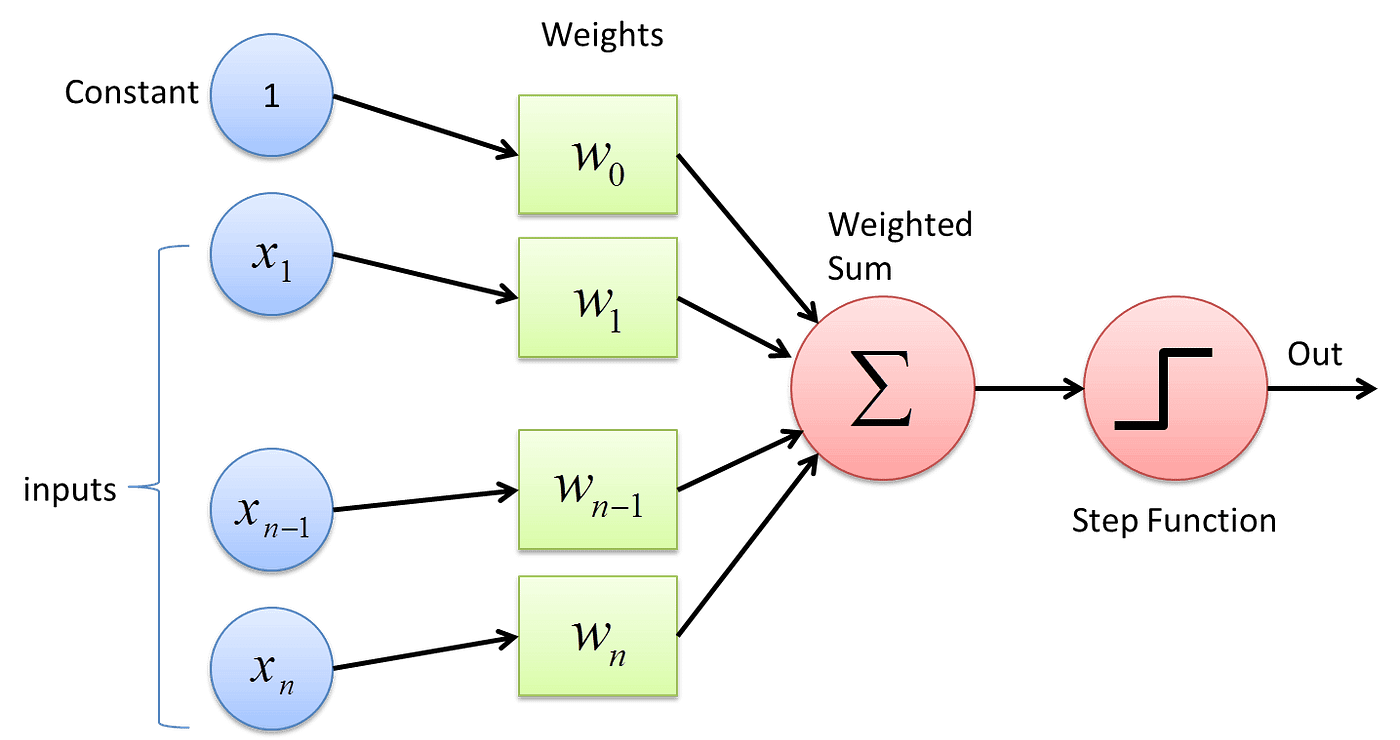
En el sentido moderno, el perceptrón es un algoritmo para aprender un clasificador binario. Es decir, una función que mapea su entrada "x" (un vector de valores reales) a un valor de salida "f(x)" (un único valor binario):
f(x) = 1 si w·x + b > 0, 0 en caso contrario
Aquí, "w" es un vector de pesos de valores reales, "w·x" es el producto punto ∑ᵢwᵢxᵢ, donde "i" abarca los índices de los vectores, y "b" es el sesgo, un término constante que no depende de ningún valor de entrada.
Ejemplo:
Aquí tienes una implementación simple de un perceptrón en Python:
import numpy as np
class Perceptron(object):
def init(self, no_of_inputs, threshold=100, learning_rate=0.01):
self.threshold = threshold
self.learning_rate = learning_rate
self.weights = np.zeros(no_of_inputs + 1) # Initialize weights to zeros
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # Include bias term
activation = 1 if summation > 0 else 0 # Simplified activation calculation
return activation
def train(self, training_inputs, labels):
for _ in range(self.threshold):
for inputs, label in zip(training_inputs, labels):
prediction = self.predict(inputs)
# Update weights including bias term
update = self.learning_rate * (label - prediction)
self.weights[1:] += update * inputs
self.weights[0] += updateEste código de ejemplo define una clase llamada Perceptron, que tiene tres métodos: __init__, predict y train. El método __init__ inicializa los atributos del objeto, el método predict predice la salida del perceptrón para una entrada dada y el método train entrena el perceptrón con un conjunto de datos de entrenamiento dado.
La salida del código dependerá de los datos de entrenamiento que utilices. Por ejemplo, si entrenas el perceptrón con un conjunto de datos de clasificación binaria, entonces la salida del método train serán un conjunto de pesos que se pueden utilizar para clasificar nuevos datos.
6.1.2 Limitaciones de un Solo Perceptrón
Aunque el perceptrón forma la base de las redes neuronales, tiene sus limitaciones. Aunque puede aprender muchos patrones, su capacidad de aprendizaje puede estar limitada por su diseño. Una de las limitaciones más significativas de un solo perceptrón es que solo puede aprender patrones linealmente separables. Esto significa que solo puede separar puntos de datos con una línea recta o un hiperplano en dimensiones superiores. Como resultado, no puede aprender fronteras de decisión más complejas. Esta es una limitación importante porque muchos problemas del mundo real no son linealmente separables y requieren fronteras de decisión más complejas que un solo perceptrón no puede aprender.
Por ejemplo, considera el problema XOR, donde tenemos cuatro puntos en un espacio 2D: (0,0), (0,1), (1,0) y (1,1). El objetivo es separar los puntos donde el XOR de las coordenadas es 1 de los puntos donde el XOR es 0. Este problema no es linealmente separable y un solo perceptrón no puede resolverlo. Por lo tanto, para resolver tales problemas, necesitamos usar una arquitectura más compleja que pueda aprender fronteras de decisión no lineales. Una de esas arquitecturas es el perceptrón de múltiples capas, que consta de múltiples perceptrones dispuestos en capas para aprender patrones más complejos.
6.1.3 Perceptrón de Múltiples Capas (MLP)
Para superar las limitaciones de un solo perceptrón y aumentar su precisión, podemos usar un perceptrón de múltiples capas (MLP). El concepto de un MLP es relativamente simple: consta de múltiples capas de perceptrones, también conocidos como neuronas, donde la salida de una capa sirve como entrada para la siguiente capa. Esta estructura permite que el MLP aprenda patrones más complejos y no lineales que un solo perceptrón no podría comprender.
Un MLP suele constar de una capa de entrada, una o más capas ocultas y una capa de salida. Cada una de estas capas consta de múltiples neuronas, y cada neurona en una capa está conectada a cada neurona en la siguiente capa. Estas conexiones están asociadas con pesos, que se ajustan durante el proceso de aprendizaje para optimizar el rendimiento del MLP.
El proceso de entrenamiento de un MLP es iterativo e implica la propagación hacia adelante y hacia atrás de la señal de entrada. Durante la propagación hacia adelante, la señal de entrada se procesa a través de las capas de neuronas, y la salida de cada capa se pasa a la siguiente capa. Durante la propagación hacia atrás, se calcula el error en la predicción y se propaga hacia atrás a través de las capas para ajustar los pesos y mejorar la precisión del MLP.
Por lo tanto, está claro que un MLP es una forma más sofisticada y poderosa de red neuronal que puede aprender y reconocer patrones complejos. Al agregar más capas y neuronas, un MLP puede entrenarse para lograr niveles más altos de precisión y puede utilizarse en diversas aplicaciones, como reconocimiento de imágenes, reconocimiento de voz y procesamiento de lenguaje natural.
Ejemplo:
Aquí tienes una implementación simple de un MLP con una capa oculta en Python utilizando la biblioteca Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer
model.add(Dense(32, input_dim=8, activation='relu'))
# Add an output layer
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tangente hiperbólica (tanh) y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X e y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial (history), que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1.4 Funciones de Activación
En el contexto de las redes neuronales, una función de activación define la salida de una neurona dado un conjunto de entradas. Inspiradas biológicamente por la actividad en nuestros cerebros donde diferentes neuronas se activan o disparan por diferentes estímulos, las funciones de activación se utilizan para añadir no linealidad al proceso de aprendizaje.
En el caso del perceptrón, utilizamos una simple función escalón como función de activación. Si la suma ponderada de las entradas es mayor que un umbral, el perceptrón se dispara y produce un 1; de lo contrario, produce un 0.
Sin embargo, esta función escalón no es adecuada para perceptrones multicapa que utilizamos en el aprendizaje profundo. La función escalón contiene solo segmentos planos, y por lo tanto, su derivada es cero. Esto es problemático porque durante la retropropagación (que discutiremos más adelante), utilizamos la derivada de la función de activación para actualizar los pesos y sesgos. Si la derivada es cero, entonces los pesos y sesgos no se actualizarán efectivamente durante el entrenamiento, y el modelo podría no aprender en absoluto.
Por lo tanto, en los perceptrones multicapa, utilizamos diferentes tipos de funciones de activación, como la función sigmoide, la función tangente hiperbólica (tanh) y la Unidad Lineal Rectificada (ReLU). Estas funciones son no lineales, continuas y diferenciables, lo que las hace adecuadas para la retropropagación.
Aquí hay una breve descripción de estas funciones de activación:
Función Sigmoide
La función sigmoide es una función matemática que mapea entradas de valores reales a un rango entre 0 y 1. Es ampliamente utilizada en el aprendizaje automático y las redes neuronales artificiales para modelar relaciones no lineales entre variables de entrada y salida.
A pesar de su utilidad, la función sigmoide sufre del problema del gradiente desvanecido, que es un problema común en el aprendizaje profundo. Este problema ocurre cuando la función sigmoide se utiliza en redes neuronales profundas con muchas capas. A medida que la entrada a la función se hace más grande, el gradiente se hace más pequeño, dificultando el entrenamiento de la red.
Para superar este problema, los investigadores han desarrollado funciones de activación alternativas, como la función ReLU, que no sufren del problema del gradiente desvanecido. Sin embargo, la función sigmoide todavía se utiliza en muchas aplicaciones debido a su simplicidad y facilidad de uso.
Función Tangente Hiperbólica (tanh)
La función tanh es similar a la función sigmoide pero aplasta la entrada a un rango entre -1 y 1. También sufre del problema del gradiente desvanecido.
La función tangente hiperbólica, también conocida como función tanh, es una función matemática que es similar a la función sigmoide. Se define como la relación entre la función seno hiperbólico y la función coseno hiperbólico. La principal diferencia entre las dos funciones es que mientras la función sigmoide aplasta la entrada a un rango entre 0 y 1, la función tanh aplasta la entrada a un rango entre -1 y 1. Esto significa que la función tanh tiene un rango de salida más amplio, lo que la hace más adecuada para ciertas aplicaciones de aprendizaje automático.
Sin embargo, la función tanh no está exenta de inconvenientes. Uno de los principales problemas con la función tanh es el problema del gradiente desvanecido, que ocurre cuando los gradientes de la función se vuelven muy pequeños. Esto puede dificultar que las redes neuronales aprendan efectivamente, especialmente cuando las entradas son grandes o la red es profunda. No obstante, la función tanh sigue siendo una opción popular para ciertos tipos de redes neuronales, especialmente aquellas que requieren salidas entre -1 y 1.
Unidad Lineal Rectificada (ReLU)
La función ReLU es la función de activación más utilizada en los modelos de aprendizaje profundo. En comparación con otras funciones de activación, como la sigmoide o la tanh, se ha encontrado que ReLU es más eficiente computacionalmente, lo que la convierte en una opción popular.
Además, se ha demostrado que ReLU mitiga el problema del gradiente desvanecido, que puede ocurrir en redes neuronales profundas cuando se utilizan ciertas funciones de activación. Esto se debe a que ReLU solo establece valores negativos en 0, mientras que deja los valores positivos sin cambios, permitiendo una mejor propagación de los gradientes.
Sin embargo, es importante señalar que ReLU puede sufrir del problema de "neurona muerta", donde las neuronas pueden volverse inactivas y producir 0 para cada entrada, resultando en una pérdida de aprendizaje. Para abordar este problema, se han desarrollado variantes de ReLU, como Leaky ReLU y Parametric ReLU, que proporcionan una pequeña pendiente para las entradas negativas, evitando que las neuronas se vuelvan completamente inactivas.
Ejemplo:
Aquí te mostramos cómo puedes implementar estas funciones de activación en un perceptrón multicapa usando Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer with sigmoid activation function
model.add(Dense(32, input_dim=8, activation='sigmoid'))
# Add a hidden layer with tanh activation function
model.add(Dense(32, activation='tanh'))
# Add a hidden layer with ReLU activation function
model.add(Dense(32, activation='relu'))
# Add an output layer with sigmoid activation function
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)
# Evaluate the model
score = model.evaluate(X, y, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una, y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tanh, y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X y y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial, que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1 Perceptrón y Perceptrón de Múltiples Capas
¡Bienvenido al emocionante y rápidamente avanzado mundo de las redes neuronales y el aprendizaje profundo! Este capítulo marca un cambio significativo en nuestro viaje a medida que nos movemos de las técnicas tradicionales de aprendizaje automático al ámbito del aprendizaje profundo, que es una subcategoría del aprendizaje automático. Debido a su potencial, el aprendizaje profundo ha estado a la vanguardia de muchos avances recientes en la inteligencia artificial, con su capacidad para habilitar autos autónomos, asistentes de voz, recomendaciones personalizadas y mucho más.
En este capítulo, comenzaremos por presentar el bloque básico de construcción de las redes neuronales: el perceptrón. Este es una estructura simple que nos puede ayudar a entender estructuras más complejas como los perceptrones de múltiples capas. Luego, avanzaremos hacia estructuras más complejas y discutiremos cómo forman la base de modelos de aprendizaje profundo más avanzados. También cubriremos los conceptos clave y principios que sustentan estos modelos, incluyendo la retropropagación (backpropagation) y el descenso de gradiente (gradient descent), que son fundamentales para el funcionamiento de las redes neuronales.
Además, después de proporcionar una base sólida en redes neuronales y aprendizaje profundo, profundizaremos en temas más avanzados, incluyendo redes neuronales convolucionales y redes neuronales recurrentes, que son esenciales para comprender cómo se pueden utilizar modelos de aprendizaje profundo en el mundo real. También exploraremos cómo se utilizan estos modelos en el procesamiento del lenguaje natural, la clasificación de imágenes y el reconocimiento de voz. Al final de este capítulo, estarás bien preparado para abordar los temas más avanzados que te esperan en el emocionante mundo del aprendizaje profundo.
¡Así que sumérgete y embarquemos en este fascinante viaje de descubrimiento!
6.1.1 El Perceptrón
El perceptrón es la forma más simple de una red neuronal. Fue introducido por Frank Rosenblatt a finales de la década de 1950. Un perceptrón toma varios inputs binarios, x1, x2, ..., y produce una única salida binaria:

En el sentido moderno, el perceptrón es un algoritmo para aprender un clasificador binario. Es decir, una función que mapea su entrada "x" (un vector de valores reales) a un valor de salida "f(x)" (un único valor binario):
f(x) = 1 si w·x + b > 0, 0 en caso contrario
Aquí, "w" es un vector de pesos de valores reales, "w·x" es el producto punto ∑ᵢwᵢxᵢ, donde "i" abarca los índices de los vectores, y "b" es el sesgo, un término constante que no depende de ningún valor de entrada.
Ejemplo:
Aquí tienes una implementación simple de un perceptrón en Python:
import numpy as np
class Perceptron(object):
def init(self, no_of_inputs, threshold=100, learning_rate=0.01):
self.threshold = threshold
self.learning_rate = learning_rate
self.weights = np.zeros(no_of_inputs + 1) # Initialize weights to zeros
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # Include bias term
activation = 1 if summation > 0 else 0 # Simplified activation calculation
return activation
def train(self, training_inputs, labels):
for _ in range(self.threshold):
for inputs, label in zip(training_inputs, labels):
prediction = self.predict(inputs)
# Update weights including bias term
update = self.learning_rate * (label - prediction)
self.weights[1:] += update * inputs
self.weights[0] += updateEste código de ejemplo define una clase llamada Perceptron, que tiene tres métodos: __init__, predict y train. El método __init__ inicializa los atributos del objeto, el método predict predice la salida del perceptrón para una entrada dada y el método train entrena el perceptrón con un conjunto de datos de entrenamiento dado.
La salida del código dependerá de los datos de entrenamiento que utilices. Por ejemplo, si entrenas el perceptrón con un conjunto de datos de clasificación binaria, entonces la salida del método train serán un conjunto de pesos que se pueden utilizar para clasificar nuevos datos.
6.1.2 Limitaciones de un Solo Perceptrón
Aunque el perceptrón forma la base de las redes neuronales, tiene sus limitaciones. Aunque puede aprender muchos patrones, su capacidad de aprendizaje puede estar limitada por su diseño. Una de las limitaciones más significativas de un solo perceptrón es que solo puede aprender patrones linealmente separables. Esto significa que solo puede separar puntos de datos con una línea recta o un hiperplano en dimensiones superiores. Como resultado, no puede aprender fronteras de decisión más complejas. Esta es una limitación importante porque muchos problemas del mundo real no son linealmente separables y requieren fronteras de decisión más complejas que un solo perceptrón no puede aprender.
Por ejemplo, considera el problema XOR, donde tenemos cuatro puntos en un espacio 2D: (0,0), (0,1), (1,0) y (1,1). El objetivo es separar los puntos donde el XOR de las coordenadas es 1 de los puntos donde el XOR es 0. Este problema no es linealmente separable y un solo perceptrón no puede resolverlo. Por lo tanto, para resolver tales problemas, necesitamos usar una arquitectura más compleja que pueda aprender fronteras de decisión no lineales. Una de esas arquitecturas es el perceptrón de múltiples capas, que consta de múltiples perceptrones dispuestos en capas para aprender patrones más complejos.
6.1.3 Perceptrón de Múltiples Capas (MLP)
Para superar las limitaciones de un solo perceptrón y aumentar su precisión, podemos usar un perceptrón de múltiples capas (MLP). El concepto de un MLP es relativamente simple: consta de múltiples capas de perceptrones, también conocidos como neuronas, donde la salida de una capa sirve como entrada para la siguiente capa. Esta estructura permite que el MLP aprenda patrones más complejos y no lineales que un solo perceptrón no podría comprender.
Un MLP suele constar de una capa de entrada, una o más capas ocultas y una capa de salida. Cada una de estas capas consta de múltiples neuronas, y cada neurona en una capa está conectada a cada neurona en la siguiente capa. Estas conexiones están asociadas con pesos, que se ajustan durante el proceso de aprendizaje para optimizar el rendimiento del MLP.
El proceso de entrenamiento de un MLP es iterativo e implica la propagación hacia adelante y hacia atrás de la señal de entrada. Durante la propagación hacia adelante, la señal de entrada se procesa a través de las capas de neuronas, y la salida de cada capa se pasa a la siguiente capa. Durante la propagación hacia atrás, se calcula el error en la predicción y se propaga hacia atrás a través de las capas para ajustar los pesos y mejorar la precisión del MLP.
Por lo tanto, está claro que un MLP es una forma más sofisticada y poderosa de red neuronal que puede aprender y reconocer patrones complejos. Al agregar más capas y neuronas, un MLP puede entrenarse para lograr niveles más altos de precisión y puede utilizarse en diversas aplicaciones, como reconocimiento de imágenes, reconocimiento de voz y procesamiento de lenguaje natural.
Ejemplo:
Aquí tienes una implementación simple de un MLP con una capa oculta en Python utilizando la biblioteca Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer
model.add(Dense(32, input_dim=8, activation='relu'))
# Add an output layer
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tangente hiperbólica (tanh) y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X e y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial (history), que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1.4 Funciones de Activación
En el contexto de las redes neuronales, una función de activación define la salida de una neurona dado un conjunto de entradas. Inspiradas biológicamente por la actividad en nuestros cerebros donde diferentes neuronas se activan o disparan por diferentes estímulos, las funciones de activación se utilizan para añadir no linealidad al proceso de aprendizaje.
En el caso del perceptrón, utilizamos una simple función escalón como función de activación. Si la suma ponderada de las entradas es mayor que un umbral, el perceptrón se dispara y produce un 1; de lo contrario, produce un 0.
Sin embargo, esta función escalón no es adecuada para perceptrones multicapa que utilizamos en el aprendizaje profundo. La función escalón contiene solo segmentos planos, y por lo tanto, su derivada es cero. Esto es problemático porque durante la retropropagación (que discutiremos más adelante), utilizamos la derivada de la función de activación para actualizar los pesos y sesgos. Si la derivada es cero, entonces los pesos y sesgos no se actualizarán efectivamente durante el entrenamiento, y el modelo podría no aprender en absoluto.
Por lo tanto, en los perceptrones multicapa, utilizamos diferentes tipos de funciones de activación, como la función sigmoide, la función tangente hiperbólica (tanh) y la Unidad Lineal Rectificada (ReLU). Estas funciones son no lineales, continuas y diferenciables, lo que las hace adecuadas para la retropropagación.
Aquí hay una breve descripción de estas funciones de activación:
Función Sigmoide
La función sigmoide es una función matemática que mapea entradas de valores reales a un rango entre 0 y 1. Es ampliamente utilizada en el aprendizaje automático y las redes neuronales artificiales para modelar relaciones no lineales entre variables de entrada y salida.
A pesar de su utilidad, la función sigmoide sufre del problema del gradiente desvanecido, que es un problema común en el aprendizaje profundo. Este problema ocurre cuando la función sigmoide se utiliza en redes neuronales profundas con muchas capas. A medida que la entrada a la función se hace más grande, el gradiente se hace más pequeño, dificultando el entrenamiento de la red.
Para superar este problema, los investigadores han desarrollado funciones de activación alternativas, como la función ReLU, que no sufren del problema del gradiente desvanecido. Sin embargo, la función sigmoide todavía se utiliza en muchas aplicaciones debido a su simplicidad y facilidad de uso.
Función Tangente Hiperbólica (tanh)
La función tanh es similar a la función sigmoide pero aplasta la entrada a un rango entre -1 y 1. También sufre del problema del gradiente desvanecido.
La función tangente hiperbólica, también conocida como función tanh, es una función matemática que es similar a la función sigmoide. Se define como la relación entre la función seno hiperbólico y la función coseno hiperbólico. La principal diferencia entre las dos funciones es que mientras la función sigmoide aplasta la entrada a un rango entre 0 y 1, la función tanh aplasta la entrada a un rango entre -1 y 1. Esto significa que la función tanh tiene un rango de salida más amplio, lo que la hace más adecuada para ciertas aplicaciones de aprendizaje automático.
Sin embargo, la función tanh no está exenta de inconvenientes. Uno de los principales problemas con la función tanh es el problema del gradiente desvanecido, que ocurre cuando los gradientes de la función se vuelven muy pequeños. Esto puede dificultar que las redes neuronales aprendan efectivamente, especialmente cuando las entradas son grandes o la red es profunda. No obstante, la función tanh sigue siendo una opción popular para ciertos tipos de redes neuronales, especialmente aquellas que requieren salidas entre -1 y 1.
Unidad Lineal Rectificada (ReLU)
La función ReLU es la función de activación más utilizada en los modelos de aprendizaje profundo. En comparación con otras funciones de activación, como la sigmoide o la tanh, se ha encontrado que ReLU es más eficiente computacionalmente, lo que la convierte en una opción popular.
Además, se ha demostrado que ReLU mitiga el problema del gradiente desvanecido, que puede ocurrir en redes neuronales profundas cuando se utilizan ciertas funciones de activación. Esto se debe a que ReLU solo establece valores negativos en 0, mientras que deja los valores positivos sin cambios, permitiendo una mejor propagación de los gradientes.
Sin embargo, es importante señalar que ReLU puede sufrir del problema de "neurona muerta", donde las neuronas pueden volverse inactivas y producir 0 para cada entrada, resultando en una pérdida de aprendizaje. Para abordar este problema, se han desarrollado variantes de ReLU, como Leaky ReLU y Parametric ReLU, que proporcionan una pequeña pendiente para las entradas negativas, evitando que las neuronas se vuelvan completamente inactivas.
Ejemplo:
Aquí te mostramos cómo puedes implementar estas funciones de activación en un perceptrón multicapa usando Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer with sigmoid activation function
model.add(Dense(32, input_dim=8, activation='sigmoid'))
# Add a hidden layer with tanh activation function
model.add(Dense(32, activation='tanh'))
# Add a hidden layer with ReLU activation function
model.add(Dense(32, activation='relu'))
# Add an output layer with sigmoid activation function
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)
# Evaluate the model
score = model.evaluate(X, y, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una, y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tanh, y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X y y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial, que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1 Perceptrón y Perceptrón de Múltiples Capas
¡Bienvenido al emocionante y rápidamente avanzado mundo de las redes neuronales y el aprendizaje profundo! Este capítulo marca un cambio significativo en nuestro viaje a medida que nos movemos de las técnicas tradicionales de aprendizaje automático al ámbito del aprendizaje profundo, que es una subcategoría del aprendizaje automático. Debido a su potencial, el aprendizaje profundo ha estado a la vanguardia de muchos avances recientes en la inteligencia artificial, con su capacidad para habilitar autos autónomos, asistentes de voz, recomendaciones personalizadas y mucho más.
En este capítulo, comenzaremos por presentar el bloque básico de construcción de las redes neuronales: el perceptrón. Este es una estructura simple que nos puede ayudar a entender estructuras más complejas como los perceptrones de múltiples capas. Luego, avanzaremos hacia estructuras más complejas y discutiremos cómo forman la base de modelos de aprendizaje profundo más avanzados. También cubriremos los conceptos clave y principios que sustentan estos modelos, incluyendo la retropropagación (backpropagation) y el descenso de gradiente (gradient descent), que son fundamentales para el funcionamiento de las redes neuronales.
Además, después de proporcionar una base sólida en redes neuronales y aprendizaje profundo, profundizaremos en temas más avanzados, incluyendo redes neuronales convolucionales y redes neuronales recurrentes, que son esenciales para comprender cómo se pueden utilizar modelos de aprendizaje profundo en el mundo real. También exploraremos cómo se utilizan estos modelos en el procesamiento del lenguaje natural, la clasificación de imágenes y el reconocimiento de voz. Al final de este capítulo, estarás bien preparado para abordar los temas más avanzados que te esperan en el emocionante mundo del aprendizaje profundo.
¡Así que sumérgete y embarquemos en este fascinante viaje de descubrimiento!
6.1.1 El Perceptrón
El perceptrón es la forma más simple de una red neuronal. Fue introducido por Frank Rosenblatt a finales de la década de 1950. Un perceptrón toma varios inputs binarios, x1, x2, ..., y produce una única salida binaria:

En el sentido moderno, el perceptrón es un algoritmo para aprender un clasificador binario. Es decir, una función que mapea su entrada "x" (un vector de valores reales) a un valor de salida "f(x)" (un único valor binario):
f(x) = 1 si w·x + b > 0, 0 en caso contrario
Aquí, "w" es un vector de pesos de valores reales, "w·x" es el producto punto ∑ᵢwᵢxᵢ, donde "i" abarca los índices de los vectores, y "b" es el sesgo, un término constante que no depende de ningún valor de entrada.
Ejemplo:
Aquí tienes una implementación simple de un perceptrón en Python:
import numpy as np
class Perceptron(object):
def init(self, no_of_inputs, threshold=100, learning_rate=0.01):
self.threshold = threshold
self.learning_rate = learning_rate
self.weights = np.zeros(no_of_inputs + 1) # Initialize weights to zeros
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # Include bias term
activation = 1 if summation > 0 else 0 # Simplified activation calculation
return activation
def train(self, training_inputs, labels):
for _ in range(self.threshold):
for inputs, label in zip(training_inputs, labels):
prediction = self.predict(inputs)
# Update weights including bias term
update = self.learning_rate * (label - prediction)
self.weights[1:] += update * inputs
self.weights[0] += updateEste código de ejemplo define una clase llamada Perceptron, que tiene tres métodos: __init__, predict y train. El método __init__ inicializa los atributos del objeto, el método predict predice la salida del perceptrón para una entrada dada y el método train entrena el perceptrón con un conjunto de datos de entrenamiento dado.
La salida del código dependerá de los datos de entrenamiento que utilices. Por ejemplo, si entrenas el perceptrón con un conjunto de datos de clasificación binaria, entonces la salida del método train serán un conjunto de pesos que se pueden utilizar para clasificar nuevos datos.
6.1.2 Limitaciones de un Solo Perceptrón
Aunque el perceptrón forma la base de las redes neuronales, tiene sus limitaciones. Aunque puede aprender muchos patrones, su capacidad de aprendizaje puede estar limitada por su diseño. Una de las limitaciones más significativas de un solo perceptrón es que solo puede aprender patrones linealmente separables. Esto significa que solo puede separar puntos de datos con una línea recta o un hiperplano en dimensiones superiores. Como resultado, no puede aprender fronteras de decisión más complejas. Esta es una limitación importante porque muchos problemas del mundo real no son linealmente separables y requieren fronteras de decisión más complejas que un solo perceptrón no puede aprender.
Por ejemplo, considera el problema XOR, donde tenemos cuatro puntos en un espacio 2D: (0,0), (0,1), (1,0) y (1,1). El objetivo es separar los puntos donde el XOR de las coordenadas es 1 de los puntos donde el XOR es 0. Este problema no es linealmente separable y un solo perceptrón no puede resolverlo. Por lo tanto, para resolver tales problemas, necesitamos usar una arquitectura más compleja que pueda aprender fronteras de decisión no lineales. Una de esas arquitecturas es el perceptrón de múltiples capas, que consta de múltiples perceptrones dispuestos en capas para aprender patrones más complejos.
6.1.3 Perceptrón de Múltiples Capas (MLP)
Para superar las limitaciones de un solo perceptrón y aumentar su precisión, podemos usar un perceptrón de múltiples capas (MLP). El concepto de un MLP es relativamente simple: consta de múltiples capas de perceptrones, también conocidos como neuronas, donde la salida de una capa sirve como entrada para la siguiente capa. Esta estructura permite que el MLP aprenda patrones más complejos y no lineales que un solo perceptrón no podría comprender.
Un MLP suele constar de una capa de entrada, una o más capas ocultas y una capa de salida. Cada una de estas capas consta de múltiples neuronas, y cada neurona en una capa está conectada a cada neurona en la siguiente capa. Estas conexiones están asociadas con pesos, que se ajustan durante el proceso de aprendizaje para optimizar el rendimiento del MLP.
El proceso de entrenamiento de un MLP es iterativo e implica la propagación hacia adelante y hacia atrás de la señal de entrada. Durante la propagación hacia adelante, la señal de entrada se procesa a través de las capas de neuronas, y la salida de cada capa se pasa a la siguiente capa. Durante la propagación hacia atrás, se calcula el error en la predicción y se propaga hacia atrás a través de las capas para ajustar los pesos y mejorar la precisión del MLP.
Por lo tanto, está claro que un MLP es una forma más sofisticada y poderosa de red neuronal que puede aprender y reconocer patrones complejos. Al agregar más capas y neuronas, un MLP puede entrenarse para lograr niveles más altos de precisión y puede utilizarse en diversas aplicaciones, como reconocimiento de imágenes, reconocimiento de voz y procesamiento de lenguaje natural.
Ejemplo:
Aquí tienes una implementación simple de un MLP con una capa oculta en Python utilizando la biblioteca Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer
model.add(Dense(32, input_dim=8, activation='relu'))
# Add an output layer
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tangente hiperbólica (tanh) y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X e y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial (history), que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1.4 Funciones de Activación
En el contexto de las redes neuronales, una función de activación define la salida de una neurona dado un conjunto de entradas. Inspiradas biológicamente por la actividad en nuestros cerebros donde diferentes neuronas se activan o disparan por diferentes estímulos, las funciones de activación se utilizan para añadir no linealidad al proceso de aprendizaje.
En el caso del perceptrón, utilizamos una simple función escalón como función de activación. Si la suma ponderada de las entradas es mayor que un umbral, el perceptrón se dispara y produce un 1; de lo contrario, produce un 0.
Sin embargo, esta función escalón no es adecuada para perceptrones multicapa que utilizamos en el aprendizaje profundo. La función escalón contiene solo segmentos planos, y por lo tanto, su derivada es cero. Esto es problemático porque durante la retropropagación (que discutiremos más adelante), utilizamos la derivada de la función de activación para actualizar los pesos y sesgos. Si la derivada es cero, entonces los pesos y sesgos no se actualizarán efectivamente durante el entrenamiento, y el modelo podría no aprender en absoluto.
Por lo tanto, en los perceptrones multicapa, utilizamos diferentes tipos de funciones de activación, como la función sigmoide, la función tangente hiperbólica (tanh) y la Unidad Lineal Rectificada (ReLU). Estas funciones son no lineales, continuas y diferenciables, lo que las hace adecuadas para la retropropagación.
Aquí hay una breve descripción de estas funciones de activación:
Función Sigmoide
La función sigmoide es una función matemática que mapea entradas de valores reales a un rango entre 0 y 1. Es ampliamente utilizada en el aprendizaje automático y las redes neuronales artificiales para modelar relaciones no lineales entre variables de entrada y salida.
A pesar de su utilidad, la función sigmoide sufre del problema del gradiente desvanecido, que es un problema común en el aprendizaje profundo. Este problema ocurre cuando la función sigmoide se utiliza en redes neuronales profundas con muchas capas. A medida que la entrada a la función se hace más grande, el gradiente se hace más pequeño, dificultando el entrenamiento de la red.
Para superar este problema, los investigadores han desarrollado funciones de activación alternativas, como la función ReLU, que no sufren del problema del gradiente desvanecido. Sin embargo, la función sigmoide todavía se utiliza en muchas aplicaciones debido a su simplicidad y facilidad de uso.
Función Tangente Hiperbólica (tanh)
La función tanh es similar a la función sigmoide pero aplasta la entrada a un rango entre -1 y 1. También sufre del problema del gradiente desvanecido.
La función tangente hiperbólica, también conocida como función tanh, es una función matemática que es similar a la función sigmoide. Se define como la relación entre la función seno hiperbólico y la función coseno hiperbólico. La principal diferencia entre las dos funciones es que mientras la función sigmoide aplasta la entrada a un rango entre 0 y 1, la función tanh aplasta la entrada a un rango entre -1 y 1. Esto significa que la función tanh tiene un rango de salida más amplio, lo que la hace más adecuada para ciertas aplicaciones de aprendizaje automático.
Sin embargo, la función tanh no está exenta de inconvenientes. Uno de los principales problemas con la función tanh es el problema del gradiente desvanecido, que ocurre cuando los gradientes de la función se vuelven muy pequeños. Esto puede dificultar que las redes neuronales aprendan efectivamente, especialmente cuando las entradas son grandes o la red es profunda. No obstante, la función tanh sigue siendo una opción popular para ciertos tipos de redes neuronales, especialmente aquellas que requieren salidas entre -1 y 1.
Unidad Lineal Rectificada (ReLU)
La función ReLU es la función de activación más utilizada en los modelos de aprendizaje profundo. En comparación con otras funciones de activación, como la sigmoide o la tanh, se ha encontrado que ReLU es más eficiente computacionalmente, lo que la convierte en una opción popular.
Además, se ha demostrado que ReLU mitiga el problema del gradiente desvanecido, que puede ocurrir en redes neuronales profundas cuando se utilizan ciertas funciones de activación. Esto se debe a que ReLU solo establece valores negativos en 0, mientras que deja los valores positivos sin cambios, permitiendo una mejor propagación de los gradientes.
Sin embargo, es importante señalar que ReLU puede sufrir del problema de "neurona muerta", donde las neuronas pueden volverse inactivas y producir 0 para cada entrada, resultando en una pérdida de aprendizaje. Para abordar este problema, se han desarrollado variantes de ReLU, como Leaky ReLU y Parametric ReLU, que proporcionan una pequeña pendiente para las entradas negativas, evitando que las neuronas se vuelvan completamente inactivas.
Ejemplo:
Aquí te mostramos cómo puedes implementar estas funciones de activación en un perceptrón multicapa usando Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer with sigmoid activation function
model.add(Dense(32, input_dim=8, activation='sigmoid'))
# Add a hidden layer with tanh activation function
model.add(Dense(32, activation='tanh'))
# Add a hidden layer with ReLU activation function
model.add(Dense(32, activation='relu'))
# Add an output layer with sigmoid activation function
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)
# Evaluate the model
score = model.evaluate(X, y, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una, y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tanh, y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X y y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial, que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1 Perceptrón y Perceptrón de Múltiples Capas
¡Bienvenido al emocionante y rápidamente avanzado mundo de las redes neuronales y el aprendizaje profundo! Este capítulo marca un cambio significativo en nuestro viaje a medida que nos movemos de las técnicas tradicionales de aprendizaje automático al ámbito del aprendizaje profundo, que es una subcategoría del aprendizaje automático. Debido a su potencial, el aprendizaje profundo ha estado a la vanguardia de muchos avances recientes en la inteligencia artificial, con su capacidad para habilitar autos autónomos, asistentes de voz, recomendaciones personalizadas y mucho más.
En este capítulo, comenzaremos por presentar el bloque básico de construcción de las redes neuronales: el perceptrón. Este es una estructura simple que nos puede ayudar a entender estructuras más complejas como los perceptrones de múltiples capas. Luego, avanzaremos hacia estructuras más complejas y discutiremos cómo forman la base de modelos de aprendizaje profundo más avanzados. También cubriremos los conceptos clave y principios que sustentan estos modelos, incluyendo la retropropagación (backpropagation) y el descenso de gradiente (gradient descent), que son fundamentales para el funcionamiento de las redes neuronales.
Además, después de proporcionar una base sólida en redes neuronales y aprendizaje profundo, profundizaremos en temas más avanzados, incluyendo redes neuronales convolucionales y redes neuronales recurrentes, que son esenciales para comprender cómo se pueden utilizar modelos de aprendizaje profundo en el mundo real. También exploraremos cómo se utilizan estos modelos en el procesamiento del lenguaje natural, la clasificación de imágenes y el reconocimiento de voz. Al final de este capítulo, estarás bien preparado para abordar los temas más avanzados que te esperan en el emocionante mundo del aprendizaje profundo.
¡Así que sumérgete y embarquemos en este fascinante viaje de descubrimiento!
6.1.1 El Perceptrón
El perceptrón es la forma más simple de una red neuronal. Fue introducido por Frank Rosenblatt a finales de la década de 1950. Un perceptrón toma varios inputs binarios, x1, x2, ..., y produce una única salida binaria:

En el sentido moderno, el perceptrón es un algoritmo para aprender un clasificador binario. Es decir, una función que mapea su entrada "x" (un vector de valores reales) a un valor de salida "f(x)" (un único valor binario):
f(x) = 1 si w·x + b > 0, 0 en caso contrario
Aquí, "w" es un vector de pesos de valores reales, "w·x" es el producto punto ∑ᵢwᵢxᵢ, donde "i" abarca los índices de los vectores, y "b" es el sesgo, un término constante que no depende de ningún valor de entrada.
Ejemplo:
Aquí tienes una implementación simple de un perceptrón en Python:
import numpy as np
class Perceptron(object):
def init(self, no_of_inputs, threshold=100, learning_rate=0.01):
self.threshold = threshold
self.learning_rate = learning_rate
self.weights = np.zeros(no_of_inputs + 1) # Initialize weights to zeros
def predict(self, inputs):
summation = np.dot(inputs, self.weights[1:]) + self.weights[0] # Include bias term
activation = 1 if summation > 0 else 0 # Simplified activation calculation
return activation
def train(self, training_inputs, labels):
for _ in range(self.threshold):
for inputs, label in zip(training_inputs, labels):
prediction = self.predict(inputs)
# Update weights including bias term
update = self.learning_rate * (label - prediction)
self.weights[1:] += update * inputs
self.weights[0] += updateEste código de ejemplo define una clase llamada Perceptron, que tiene tres métodos: __init__, predict y train. El método __init__ inicializa los atributos del objeto, el método predict predice la salida del perceptrón para una entrada dada y el método train entrena el perceptrón con un conjunto de datos de entrenamiento dado.
La salida del código dependerá de los datos de entrenamiento que utilices. Por ejemplo, si entrenas el perceptrón con un conjunto de datos de clasificación binaria, entonces la salida del método train serán un conjunto de pesos que se pueden utilizar para clasificar nuevos datos.
6.1.2 Limitaciones de un Solo Perceptrón
Aunque el perceptrón forma la base de las redes neuronales, tiene sus limitaciones. Aunque puede aprender muchos patrones, su capacidad de aprendizaje puede estar limitada por su diseño. Una de las limitaciones más significativas de un solo perceptrón es que solo puede aprender patrones linealmente separables. Esto significa que solo puede separar puntos de datos con una línea recta o un hiperplano en dimensiones superiores. Como resultado, no puede aprender fronteras de decisión más complejas. Esta es una limitación importante porque muchos problemas del mundo real no son linealmente separables y requieren fronteras de decisión más complejas que un solo perceptrón no puede aprender.
Por ejemplo, considera el problema XOR, donde tenemos cuatro puntos en un espacio 2D: (0,0), (0,1), (1,0) y (1,1). El objetivo es separar los puntos donde el XOR de las coordenadas es 1 de los puntos donde el XOR es 0. Este problema no es linealmente separable y un solo perceptrón no puede resolverlo. Por lo tanto, para resolver tales problemas, necesitamos usar una arquitectura más compleja que pueda aprender fronteras de decisión no lineales. Una de esas arquitecturas es el perceptrón de múltiples capas, que consta de múltiples perceptrones dispuestos en capas para aprender patrones más complejos.
6.1.3 Perceptrón de Múltiples Capas (MLP)
Para superar las limitaciones de un solo perceptrón y aumentar su precisión, podemos usar un perceptrón de múltiples capas (MLP). El concepto de un MLP es relativamente simple: consta de múltiples capas de perceptrones, también conocidos como neuronas, donde la salida de una capa sirve como entrada para la siguiente capa. Esta estructura permite que el MLP aprenda patrones más complejos y no lineales que un solo perceptrón no podría comprender.
Un MLP suele constar de una capa de entrada, una o más capas ocultas y una capa de salida. Cada una de estas capas consta de múltiples neuronas, y cada neurona en una capa está conectada a cada neurona en la siguiente capa. Estas conexiones están asociadas con pesos, que se ajustan durante el proceso de aprendizaje para optimizar el rendimiento del MLP.
El proceso de entrenamiento de un MLP es iterativo e implica la propagación hacia adelante y hacia atrás de la señal de entrada. Durante la propagación hacia adelante, la señal de entrada se procesa a través de las capas de neuronas, y la salida de cada capa se pasa a la siguiente capa. Durante la propagación hacia atrás, se calcula el error en la predicción y se propaga hacia atrás a través de las capas para ajustar los pesos y mejorar la precisión del MLP.
Por lo tanto, está claro que un MLP es una forma más sofisticada y poderosa de red neuronal que puede aprender y reconocer patrones complejos. Al agregar más capas y neuronas, un MLP puede entrenarse para lograr niveles más altos de precisión y puede utilizarse en diversas aplicaciones, como reconocimiento de imágenes, reconocimiento de voz y procesamiento de lenguaje natural.
Ejemplo:
Aquí tienes una implementación simple de un MLP con una capa oculta en Python utilizando la biblioteca Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer
model.add(Dense(32, input_dim=8, activation='relu'))
# Add an output layer
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tangente hiperbólica (tanh) y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X e y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial (history), que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.
6.1.4 Funciones de Activación
En el contexto de las redes neuronales, una función de activación define la salida de una neurona dado un conjunto de entradas. Inspiradas biológicamente por la actividad en nuestros cerebros donde diferentes neuronas se activan o disparan por diferentes estímulos, las funciones de activación se utilizan para añadir no linealidad al proceso de aprendizaje.
En el caso del perceptrón, utilizamos una simple función escalón como función de activación. Si la suma ponderada de las entradas es mayor que un umbral, el perceptrón se dispara y produce un 1; de lo contrario, produce un 0.
Sin embargo, esta función escalón no es adecuada para perceptrones multicapa que utilizamos en el aprendizaje profundo. La función escalón contiene solo segmentos planos, y por lo tanto, su derivada es cero. Esto es problemático porque durante la retropropagación (que discutiremos más adelante), utilizamos la derivada de la función de activación para actualizar los pesos y sesgos. Si la derivada es cero, entonces los pesos y sesgos no se actualizarán efectivamente durante el entrenamiento, y el modelo podría no aprender en absoluto.
Por lo tanto, en los perceptrones multicapa, utilizamos diferentes tipos de funciones de activación, como la función sigmoide, la función tangente hiperbólica (tanh) y la Unidad Lineal Rectificada (ReLU). Estas funciones son no lineales, continuas y diferenciables, lo que las hace adecuadas para la retropropagación.
Aquí hay una breve descripción de estas funciones de activación:
Función Sigmoide
La función sigmoide es una función matemática que mapea entradas de valores reales a un rango entre 0 y 1. Es ampliamente utilizada en el aprendizaje automático y las redes neuronales artificiales para modelar relaciones no lineales entre variables de entrada y salida.
A pesar de su utilidad, la función sigmoide sufre del problema del gradiente desvanecido, que es un problema común en el aprendizaje profundo. Este problema ocurre cuando la función sigmoide se utiliza en redes neuronales profundas con muchas capas. A medida que la entrada a la función se hace más grande, el gradiente se hace más pequeño, dificultando el entrenamiento de la red.
Para superar este problema, los investigadores han desarrollado funciones de activación alternativas, como la función ReLU, que no sufren del problema del gradiente desvanecido. Sin embargo, la función sigmoide todavía se utiliza en muchas aplicaciones debido a su simplicidad y facilidad de uso.
Función Tangente Hiperbólica (tanh)
La función tanh es similar a la función sigmoide pero aplasta la entrada a un rango entre -1 y 1. También sufre del problema del gradiente desvanecido.
La función tangente hiperbólica, también conocida como función tanh, es una función matemática que es similar a la función sigmoide. Se define como la relación entre la función seno hiperbólico y la función coseno hiperbólico. La principal diferencia entre las dos funciones es que mientras la función sigmoide aplasta la entrada a un rango entre 0 y 1, la función tanh aplasta la entrada a un rango entre -1 y 1. Esto significa que la función tanh tiene un rango de salida más amplio, lo que la hace más adecuada para ciertas aplicaciones de aprendizaje automático.
Sin embargo, la función tanh no está exenta de inconvenientes. Uno de los principales problemas con la función tanh es el problema del gradiente desvanecido, que ocurre cuando los gradientes de la función se vuelven muy pequeños. Esto puede dificultar que las redes neuronales aprendan efectivamente, especialmente cuando las entradas son grandes o la red es profunda. No obstante, la función tanh sigue siendo una opción popular para ciertos tipos de redes neuronales, especialmente aquellas que requieren salidas entre -1 y 1.
Unidad Lineal Rectificada (ReLU)
La función ReLU es la función de activación más utilizada en los modelos de aprendizaje profundo. En comparación con otras funciones de activación, como la sigmoide o la tanh, se ha encontrado que ReLU es más eficiente computacionalmente, lo que la convierte en una opción popular.
Además, se ha demostrado que ReLU mitiga el problema del gradiente desvanecido, que puede ocurrir en redes neuronales profundas cuando se utilizan ciertas funciones de activación. Esto se debe a que ReLU solo establece valores negativos en 0, mientras que deja los valores positivos sin cambios, permitiendo una mejor propagación de los gradientes.
Sin embargo, es importante señalar que ReLU puede sufrir del problema de "neurona muerta", donde las neuronas pueden volverse inactivas y producir 0 para cada entrada, resultando en una pérdida de aprendizaje. Para abordar este problema, se han desarrollado variantes de ReLU, como Leaky ReLU y Parametric ReLU, que proporcionan una pequeña pendiente para las entradas negativas, evitando que las neuronas se vuelvan completamente inactivas.
Ejemplo:
Aquí te mostramos cómo puedes implementar estas funciones de activación en un perceptrón multicapa usando Keras:
from keras.models import Sequential
from keras.layers import Dense
import numpy as np
# Placeholder data (replace with your actual data)
X = np.random.rand(100, 8)
y = np.random.randint(2, size=(100, 1))
# Create a Sequential model
model = Sequential()
# Add an input layer and a hidden layer with sigmoid activation function
model.add(Dense(32, input_dim=8, activation='sigmoid'))
# Add a hidden layer with tanh activation function
model.add(Dense(32, activation='tanh'))
# Add a hidden layer with ReLU activation function
model.add(Dense(32, activation='relu'))
# Add an output layer with sigmoid activation function
model.add(Dense(1, activation='sigmoid'))
# Compile the model
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
# Fit the model
model.fit(X, y, epochs=150, batch_size=10)
# Evaluate the model
score = model.evaluate(X, y, verbose=0)
print('Test loss:', score[0])
print('Test accuracy:', score[1])
Este código de ejemplo crea un modelo secuencial con una capa de entrada de 8 neuronas, tres capas ocultas con 32 neuronas cada una, y una capa de salida de 1 neurona. La primera capa oculta utiliza activación sigmoide, la segunda capa oculta utiliza activación tanh, y la tercera capa oculta utiliza activación ReLU. El modelo se compila con pérdida de entropía cruzada binaria, optimizador Adam y métricas de precisión. El modelo se ajusta a los datos X y y durante 150 épocas con un tamaño de lote de 10.
La salida del código será un objeto de historial, que contiene información sobre el proceso de entrenamiento, como la pérdida y la precisión en cada época. Puedes utilizar el objeto de historial para evaluar el rendimiento del modelo y seleccionar los mejores hiperparámetros.

